First it's normal to assume that air resistance doesn't matter, because the projectile is heavy, it is aerodynamic, or the time of flight is so short that air resistance makes no difference. This may be unrealistic but it is good enough for game simulations, and makes the mathematics solvable.
The other assumption is that the target is no higher or lower than the launcher, so they are at the same height. This is more a constraint than a simplifying assumption but it's one that works well for many game types, where e.g. all combatants fight on the same level. It greatly simplifies the mathematics.
With these two assumptions there are a number of calculations that can be done. One is the maximum range of a projectile, for a given launch speed. This depends on the gravity (g) and speed (v) and equals
With these two assumptions there are a number of calculations that can be done. One is the maximum range of a projectile, for a given launch speed. This depends on the gravity (g) and speed (v) and equals
This is achieved by launching the projectile at 45°; any other angle and it won't go so far. This leads to the obvious question: what angle should it be launched at to travel another, shorter distance?
There are actually two answers to this, the above angle α and 90° - α. The smaller angle α gives the shorter path and time of flight. The other angle gives a more exaggerated path, useful for clearing barriers or for dramatic effect.
Both are shown in the following animation, hosted on Wonderfl where you can view and edit the code. Click to set the range, click again for it to use the other angle to reach the target. The code is fairly minimal, just showing the projectile, path and angle.

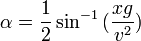
No comments:
Post a Comment